I call heaven and earth to witness against you this day, that I have set before thee life and death, the blessing and the curse: therefore choose life, that thou mayest live, thou and thy seed;
That’s from The Bible; Deuteronomy 30:19.
I’ve just watched the final episode of Carl Sagan’s “Cosmos: A Personal Voyage“. There’s a load of fanboyism surrounding “Cosmos” – and indeed anything to do with Sagan – but I believe that the hype is justified. Few things have ever so inspired me.
According to Sagan, “the cosmos is all that is or ever was or ever will be”. A series of 13 1-hour episodes clearly can not tell us all that, but Sagan explainsenough about the Big Bang, space, life, and the history of humanity and science to leave ones mind filled with copious measures of understanding… and wonder. In my opinion, Sagan’s goal with Cosmos is to convey the context of humanity’s existence and, in doing so, inspire us to continue moving forward; building on the past. I think he was successful.
The final episode of “Cosmos” – the one I watched this evening – is called “Who Speaks for Earth?”, and it opens with the Bible quotation which I included before. I don’t consider The Bible to be sacred ((I’m an atheist.)), but I’m not afraid to enjoy certain passages, and I think this particular verse fitted Sagan’s message perfectly – as must he ((Yes, I’m writing in the wrong tense. I don’t care.)). Although the choice might not have been provided by God, it is the same: either we can use our science and technology for our continuation and improvement, or we can use it to for our destruction ((By nuclear war, for example.)). It is ours to make ((I realise that we are in much less imminent danger than was the world at the time of the creation of “Cosmos”, but it’s still possible (maybe even likely) that the human branch of the tree of life will fall by its own hand. We – meaning humanity – have to unite. As Sagan says towards the end of the episode: “…an organism at war with itself is doomed. We are one planet.” He’s right you know.)).
Photo Credit: NASA/ESA and The Hubble Heritage Team STScI/AURA
NB: If you’re just interested in the maths, click here.
My most loyal reader and commenter, Sir Terry Kumblemann requested:
“Posts about maths (seriously). To be more specific, sequences like the Fibonacci sequence and similar (or completely crazy sequences).”
Now, I’m into maths, particularly all things patterny and numbery, but is my knowledge suitable for blog posts? I know that there are many crazy sequences – I could reel off the first 20 numbers of a sequence ((The Fibonacci sequence is particularly interesting, popping up all over nature as if by magic. But I wouldn’t give it justice if I wrote about it now, with Wikipedia as my sole reference material.)) and say what the pattern is – but I’d need to put quite a lot of thought and research into my posts. That’s fine, but not right now.
Don’t worry though, I will get to it eventually. I suppose mathematics could become a focus for this blog ((Here goes the obligatory blogging about blogging paragraph.)). I have plenty of anecdotes and other stories to tell, but most of them will end up needing the footnote “…you had to be there” once I’ve attempted to write them up. I’m hoping to begin a masters degree in pure mathematics next year, so it might be useful to keep thinking about the subject whilst I’m on my gap year ((I’m enjoying it very much, thanks for asking. I just wish it was a bit warmer.)). We’ll see.
Today I’ll talk about fractals. The inspiration for my substitute topic comes from another episode of Horizon. I’ve written about Horizon a few times before, after watching episodes on particularly intriguing topics which I thought were well done.
Sadly, I can’t say that the rest of the current series of Horizon has been as good as “The Secret You” ((Not the highest bar to pass, either.)). Read my reviews in this post ((I had to split them off from here because this post was getting too long.)).

Right. My reviews of Horizon over, I can now focus on fractals. In “How Long is a Piece of String?”, Alan Davies was attempting to get the definitive length of his string. During the Marcus du Sautoy segment, Marcus tried to demonstrate that Alan’s string could have an infinitely long perimeter ((Not exactly its length, but near enough.)).
He did this by trying to get Alan to measure the length of a stretch of Britain’s coastline with a ruler. Alan gave a length. Marcus then asked Alan to do this again with a piece of string, and then with an even more accurate device. Each time, the measured length increased. That’s because Alan was able to measure more detail – the ‘resolution’ of his measuring device increased so that he could take into account the extra length in coastline caused by smaller and smaller distortions in the coast. Marcus’s point is that – at least with a coastline – the more accurate your measuring device, the larger the measured coastline.
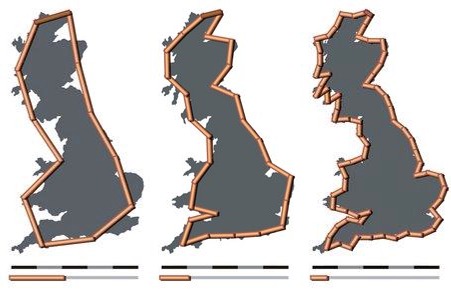
Have a look at these images on Wikipedia’s article on Mandelbrot’s paper “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension” ((Read up about the Coastline Paradox too, if you’d like.)). It shows that the measured coastline depends on how small the smallest measurable length of your ‘ruler’ is. Why stop at something that can measure objects 100 metres across? Why stop at 10 metres? Why stop at a grain of sand? Every time you go smaller, you measure a longer coastline.
I hope that I’ve communicated this concept. If you haven’t followed so far, let me know. I should have demonstrated how something – Great Britain, or Alan’s string – could have a definite area ((For example, Britain would fit into a square with a side of 1,000 miles, therefore its area is less than 1,000,000 square miles.)), but could be bounded by an infinite perimeter.
This is what you can think of fractals as being – geometric shapes with an infinite perimeter. There’s more to them than that, of course, such as the zoomed in version looking like the zoomed out version (only it’s smaller), but I don’t want to go into too much depth right now.
In the Horzion episode, Marcus then went on to demonstrate the infinite perimeter concept by drawing a fractal in the sand. He decided to draw the Koch Snowflake – one of the simplest fractals. I will try to describe how the Koch Snowflake is formed, and then calculate some of its properties.
How to make a Koch Snowflake:
- Take an equilateral triangle – one with all 3 sides the same length.
- Mentally split each side into thirds.
- On the middle third of each side, place an equaliteral triangle (the length of side being that of a third from number 2).
- Go to number 2.
- You will never get to number 5.
Again, stolen from Wikipedia, is an image. It depicts the initial equaliteral triangle, and then the state of the fractal after each of the first three passes through my loop:
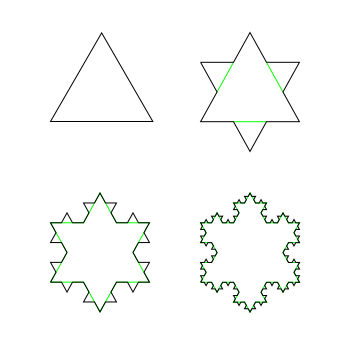
Have an animated version, too:

Perimeter
How much has the perimeter of the fractal increased each time? This can be worked out by imagining each side as consisting of 3 equal thirds. After each pass, the outside 2 thirds of the side remain the same; the middle 1 third, however, is converted into 2 thirds by the addition of an equaliteral triangle of length 1 third ((2 sides of length 1 third are showing instead of the original section of length 1 third.)). Therefore, each side has increased from 3/3 in length to 4/3 in length – that is, it’s 4/3 times bigger, and, by extension, the perimeter of the whole fractal has increased by 4/3 ((Due to the nature of this fractal, every side has the same transformation applied to it at once. Therefore, as one side increases by 4/3, every side increases by 4/3. This means that the whole perimeter has increased by this amount.)).
What happens to the perimeter as we keep going through my loop? The initial equilateral triangle has a perimeter of 3 × the length of the triangle’s side, or 3l. Then, after the first pass, the length is 3l × 4/3. After the second pass, the perimeter increases by 4/3 again, so it is 3l × 4/3 × 4/3, or 3l × (4/3)2, and the third time it is 3l × (4/3)3.
So, when we have gone through the loop an infinite number of times, the perimeter is 3l × (4/3)infinity, which is infinitely large ((That is because (4/3)x gets bigger by a bigger amount each time you increase x; therefore it is not going to approach a limit – basically, that only happens when something is getting bigger by a decreasing amount each time, until that decreasing amount is 0. In this case, it increases without bound, so is infinite.)). Therefore, the perimeter of the Koch Snowflake is infinite.
Area
But the area is not infinite. The area of a triangle is calculated by 1/2 × base × height or 1/2 ab sin C, where a and b are adjacent sides, and C is the angle between them. In our initial equilateral triangle, with side length l and angle 60° ((The angles in an equaliteral triangle are always all equal to 60°.)), the area is 1/2 × l × l × sin 60°:
Area of the initial triangle ((Through simplification.)) = root 3/4 × l2. I shall abbreviate this to A.
The first time we pass through my fractal recipe loop, the initial triangle stays the same; however, we add 3 new, smaller equilateral triangles, whose length is a third that of the initial triangle.
Area of new triangles = 3 × root 3/4 × (1/3l)2
Area of new triangles = 1/3 × A ((Through simplification.))
The total area is the area of the initial triangle plus the area of the 3 new triangles:
Total area = A + 1/3 A
The second time we go through the loop, we are now adding 12 triangles, as you can see from the above diagram. The length of each new triangle is a third that of the previously added triangle, itself a third that of the initial triangle. So the length of these new triangles is 1/9l.
Area of new triangles = 12 × root 3/4 × (1/9l)2
Area of new triangles = 4/27 × A ((Through simplification.))
So Total area = A + 1/3 A + 4/27 A
I’ll add a few more terms:
Total area = A + 1/3 A + 4/27 A + 16/243 A + 64/2187 A + …
Here we have a sum which would give us the total area of the Koch Snowflake. It is called a geometric series, because (ignoring the first term), there is a common ratio between adjacent terms. You can find that ratio by dividing one term by the previous term, but we can see it here simply by looking: to get the next term, multiply the current one by 4 (that shows in the progression of 1… 4… 16… 64…) and then divide it by 9 (that shows in the progression of 1/3… 1/27… 1/243… 1/2187…). Therefore, the common ration is 4/9.
This is great – the common ratio is less than 1 and greater than -1 (-1 < ratio < 1). This means that work out what area is given when all the infinite terms of this geometric series are added up!
Our initial value is 1/3 A (we’re ignoring the first term, A, as it does not fit into the geometric series), and the common ratio of 4/9. To calculate the sum to infinity of this series, we divide the initial value by 1 – r (where r is the common ratio).
1/3 A ÷ 5/9 = 3/5 A
This is the sum of the geometric series! To find the total area of the Koch Snowflake, we must remember to add back in the first term (A) as we were ignoring it a minute ago. Therefore:
Total area of Koch Snowflake = 3/5 A + A = 8/5 A
- Now, remember, A = root 3/4 × l2
Total area of Koch Snowflake = 8/5 × root 3/4 × l2
Total area of Koch Snowflake = 2/5 × l2 × root 3 ((Through simplification.))
Or, as Wikipedia says ((They used s instead of l.)):
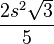
As you can see, that is definitely not an infinite number. For example, if you chose s to be the fourth root of 3 – that is, if the length of side of the initial triangle used in my recipe was 3^1/4 – then the area of this shape which has an infinite perimeter is 6/5 square units. Incredible.
So how was that? To basic? To complicated? Too long winded? Not clear enough? Let me know.
STOP PRESS: Mr Kimberly adds:
“On second thoughts. Do a post about Infinity.”
Good idea.
After writing the post “Remembrance” ((Let’s blog about blogging! Yay!)), and conversing with Mr. Kimble-Wimble in the comments section, I realised that it was bullshit. I started off writing with only a vague feeling – that Remembrance Day is a bit silly – and my lack of structured thinking resulted in a mess of a post with no clear point. I’ll be a bit more disciplined with myself.
I’ve been reading a lot lately, mostly blogs through my RSS reader ((NetNewsWire for iPhone, which links up with Google Reader)), as well as a couple of books. In the near 2-months that I’ve been using Google Reader rather than NewsGator, my starred items list has swelled to over 400 items, so I shall soon sift through that, and create a post containing links to the few gems that I eventually find – as much for my benefit as anyone else’s ((Amongst other things, I’ll share articles about writing, articles about reading articles about writing, and articles about reading articles about reading articles about writing.)).
Several exciting things have happened in my life recently:
- I’ve applied to study various mathsy degrees at university. I’ll go to St Andrews if they make me an offer. Last year, having excellent grades but no idea of where I wanted to study, I applied to Cambridge only. I didn’t get in, but I’ve had nearly a year now to ponder things and I think I’ve submitted a strong application.
- I went past Haddows the other day, and saw that they were closing down. I’d seen a report about their bankruptcy on TV a few weeks ago, and I assumed that all the stores would have closed by now. I didn’t even know that there was a Haddows store here. Anyway, I went in and got 12 cans of Kopparberg for £9 (40% off!) and a block of galaxy for 40p (75% off!).
- I also spent a day helping someone to set up their new 32GB iPhones 3GS and to show them around the iPhone OS. I’d never spent more than a few minutes playing with an iPhone – I only have my only 26 month iPod Touch experience – and it really is a great piece of hardware and software. Someone else I know described their iPhones as “life-changing”, and although it’s not life-changing like winning the lottery, my iPod really has changed the way that I interact with the internet and my digital content. It’s great.
- I went along to the local speaker’s club with George, at his suggestion, and I was treated to a speech about not knowing what subject to give a speech on!
- Being a typical Sunday, it’s rained all day.
I also currently have 38 draft posts ready to finish ((Well, most of them are just titles still, but they’ll be good. Every time I remember an anecdote or have another good idea for a blog post, I write it down to preserve the thought.)). Titles include: Your Most Valuable Possession #2, Suspicious Either Way, and a story about the time I Met Noel Sharkey.
Now to watch Top Gear.












